Yüksek lisans tez analizlerini SPSS ile doktora tez uygulamasını RapidMiner ile yapmış biri olarak neden R?
Bana göre aslında kullandığınız “tool(*)”un bir önemi yok!!! Eğer ne yapmak istediğinizi iyi biliyorsanız kullandığınız araç çok da sorun değil! Sadece yapmak istediğiniz analizlere ve cebinizdeki paraya göre şekillenmekte bu araç (tool) seçimi.
Çoğu istatistik analiz için SPSS gayet yeterli bir araç. Ancak ücretli bir yazılım olduğu için herkes kolaylıkla SPSS’e erişememekte. Ben şanslıyım ki üniversitemin SPSS 21.0 sürümü için lisans anlaşması var ve çoğu istatistik analizi gerçekleştirebiliyorum (ancak üniversitemin SPSS’in veri madenciliği yazılımı olan Modeler anlaşması yok o yüzden veri madenciliği için SPSS’i tercih edemiyorum).
Veri madenciliği için de ne yalan söyleyeyim RapidMiner işimi görmekte (RapidMiner yazılarım da gelecek ne de olsa kaç sene kahrımı çekti )
Peki neden R?
Kullandığımız aracın önemi yok dedik. Önemi yoksa birkaç tıkla analizlerimizi gerçekleştirebilecek iken neden kod yazma zahmetine girelim? Veri-güdümlü bir çağda yaşamaktayız (çok klasik bir cümleydi burada da yazmazsam çatlardım :)). Veri yapıları değişmekte, çeşitlenmekte… Veri yapıları çeşitlendikçe analiz için gerekli algoritmalar da çeşitlenmekte, gelişmekte (ayrıntı için buraya bir bakınız ;)). Bu gelişmelere nasıl ayak uydursak peki? İşte R bunun için biçilmiş kaftan. R’ı öğrenmek ve uygulamak da artık bir ayrıcalık değil açıkçası bir zorunluluk haline gelmekte… SPSS, RapidMiner ve bir çok yazılım artık R eklentileri de eklemiş bulunmakta sistemlerine. Ha en önemlisi de R ücretsiz Peki R bilmek yeterli mi? R, bir çok konuda size yetecektir ancak hazır başlamışken bir de Python’a da el atmak işinize yarayacaktır. Python’ın önemine de ilerleyen yazılarımızda değineceğiz Şimdilik R ve basit istatistik uygulamalardan başlayıp ileri veri madencilik uygulamalarında kullanımlarına odaklanacağız.
R ile ilgili binlerce web sayfası, sayısız kitap bulunmakta. Ancak bunların çoğu İngilizce. Türkçe kaynak yetersizliği ve İngilizceye olan hakimiyetsizlik genç araştırmacılar için problem olabilmekte. Özetle Türkçe kaynaklara bir katkım olsun amacıyla bu yazılara başlamış oldum. Aslında itiraf etmek gerekirse bu yazılar kendime not. Bazen üzerinde çok uğraştığınız bir analizin aşamalarını üzerinden zaman geçtikçe hatırlamakta zorlanabiliyorsunuz. Bilgiye dönüştürdüğünüz deneyimler çok kıymetli ve kolay erişilebilir olması değerini daha da arttırmakta… Bilginin paylaşılması gerektiğine inanan ben, size de bir kıyak çekiyorum işte… Hayrını görünüz
R ile Hiyerarşik Kümeleme!
Kümeleme, gözlemlerden (nesnelerden) meydana gelmiş verileri kullanarak,benzer nesneleri gruplamaktır [1]. Kümeleme Analizi, X veri matrisinde yer alan ve doğal gruplamaları kesin olarak bilinmeyen birimleri, değişkenleri ya da birim ve değişkenleri birbirleri ile benzer olan alt kümelere (grup, sınıf) ayırmaya yardımcı olan yöntemler topluluğudur. Birimleri, değişkenler arası benzerlik (similarity) ya da farklılıklara (dissimilarity) dayalı olarak hesaplanan bazı ölçülerden yararlanarak homojen gruplara bölmek amacıyla kullanılır [2]. Kümeleme Analizinin amaçları esas olarak, bireylerin tüm değişkenler itibariyle benzerliklerini esas alarak benzer bireylerin aynı gruplarda veya kümelerde toplanması, bu kümelerin tanımlanması ve yeni bireylerin hangi gruba dahil olduğunun tahmin edilmesidir [3]. Uzaklık ölçüleri en yaygın olarak kullanılan benzerlik ölçüleridir. Kümeleme; iki birimin benzerlikleri (yakınlıkları) veya benzemezlikleri (uzaklıkları) temel alınarak yapılır [5]. Aşağıdaki şekil buna örnek olarak verilmiştir [4].
Kümeleme analizinde veriler düzenlendikten sonra uzaklık ölçülerinden yararlanılarak uzaklıklar matrisi elde edilir. Eğer analiz edilecek veriler aralık veya oran ölçekli ise, en çok kullanılan uzaklık ölçüleri, Öklit, Karaleri alınmış Öklit, Minkowski ve Manhattan City-Blok’dur. Eğer veriler sınıflayıcı (nominal) veya sıralayıcı (ordinal) ölçekli ise kullanılan uzaklık ölçüleri; Ki-kare ve Normalleştirilmiş Ki-kare olarak bilinen Phi-Karedir. Uzaklıklar matrisi elde edildikten sonra, kümeleme yönteminin seçimi söz konusudur. Bu bağlamda en yaygın olarak kullanılan yöntemler hiyerarşik ve hiyerarşik olmayan yöntemler olarak ikiye ayrılır. Hiyerarşik ve hiyerarşik olmayan yöntemler birbirlerini tamamlayıcı özelliğe sahiptirler [6].
Hiyerarşik kümeleme yöntemlerinde kümeler ardarda birleştirilir ve bir grup diğeri ile bir kez birleştirildikten sonra, devam eden adımlarda bir daha ayrılmaz. Bu yöntemler ele alınan değişkenler için hiyerarşik bir yapı oluşturmaktadırlar. Hiyerarşik kümeleme yöntemlerinde küme sayısına görsel olarak karar verilmektedir [6]. Bu durumda genellikle Dendrogram olarak bilinen ağaç diyagramı kullanılır [7].
Çeşitli hiyerarşik kümeleme yöntemleri vardır. En sık kullanılan hiyerarşik kümeleme yöntemleri [8];
- Ortalama Yöntemi (Centroid Method)
2. Tek Bağlantı (Single-Linkage Method / Nearest-Neighbor)
3. Tam Bağlantı (Complete-Linkage Method / Farthest-Neighbor)
4. Ortalama Bağlantı (Average-Linkage Method)
5. Ward Bağlantı (Ward‟s Method) dır.
Hiyerarşik Olmayan Kümeleme Yöntemleri ise, birimlerin kendi içinde homojen ve kendi aralarında heterojen olan kümelere ayrılmasını hedefleyen ve prototip kümeler aracılığı ile alt kümelerin parametre tahminlerini yapmayı (grup ya da küme ortalama vektörleri ve kovaryans matrisleri) amaçlayan yöntemlerdir. HiyerarĢik olmayan kümeleme yöntemleri arasında en yaygın kullanılanları K-Ortalamalar Kümeleme (K-Means Clustering), Medoid Kümeleme (Medoid Clustering), Fuzzy Kümeleme (Fuzzy Clustering) ve Yığma Kümeleme (Hill Climbing) yöntemleridir.
Kaynaklar:
[1] George A.F. Seber, Multivariate Observations, USA, 1984.
[2] Kazım Özdamar, Paket Programlar ile İstatistiksel Veri Analizi, Kaan Kitabevi, Eskişehir, 2004.
[3] Kemal Kurtuluş, Pazarlama Araştırmaları, Literatür Yayıncılık, İstanbul, 2004.
[4] Brian S. Everitt, An R and S-Plus Companion to Multivariate Analysis, 2005.
[5] Joseph F. Hair, Ralph E.Anderson, Ronald L. Tatham, William C.Black, Multivariate Data Analysis, Prentice Hall Int, 5th Edition, 1998.
[6] Richard Johnson, Dean W. Wichern, Applied Multivariate Statistical Analysis, 3.th ed., Prentice Hall, 1992.
[7] Brian Everitt, Graham Dunn, Applied Multivariate Data Analysis, Oxford University Press, 1992.
[8] Subhash Sharma, Applied Multivariate Techniques, John Wiley & Sons, 1996.
Uygulama:
İlk R uygulaması olarak hiyerarşik kümelemeyi seçtim. Hiyerarşik kümeleme küme sayısını bilmediğimiz durumlarda bize yardımcı olan bir yöntem. Hiyerarşik kümelemenin çıktısı olan “dendrogram” denilen ağaç grafikleriyle kümelenmeleri görselleştirip küme sayılarına karar verebilmekteyiz. Mümkün hiyerarşik kümeleme yöntemleri (ortalama, tek, vs.) değişik uzaklık hesaplama ölçüleri (öklid, kareli öklid, vs.) ile gerçekleştirilmekte, en uygun küme yapısını veren yöntem seçilmektedir.
Uygulamada R’daki hazır veri setlerinden “mtcars” kullanılmıştır. 32 birim 11 nitelikten (**) oluşan veri setinde birimler araba modelleri, nitelikler de arabaların özelliklerini temsil etmektedir. Uygulamada istenilen; benzer özellikteki araba modellerini aynı gruplarda toplamaktır.
(*) eğer veri madenciliği ile ilgileniyorsanız size sorulacak birinci ya da ikinci soru şudur: “hangi tool’u kullanıyorsun?” plaza türkçesi gibi olmasa da bir çok türkçeleştirilemeyen kelimeyle karşılaşmamız çok çoook olası ne yazık ki
(**) birim, nitelik, değişken vs. gibi tanımlar istatistik, veri madenciliği, makine öğrenmesi gibi alanlarda farklı isimlerle anılmakta. Bunu da veri yapıları yazımda açıklayacağım…
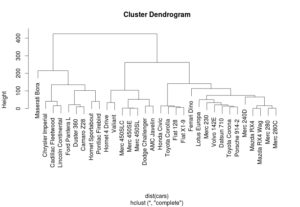
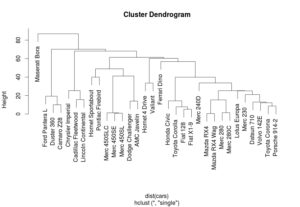
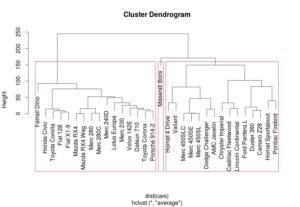
Uygulamada öncelikle mtcars verisini çağırıyoruz. Sonrasında da hiyerarşik kümeleme fonksiyonuyla (hclust() ) dendrogramlar çizdiriyoruz. İlk örnek için ortalama (ave), ikinci örnek için tam (complete), üçüncü için ise tek (single) bağlantı yöntemleri seçilmiştir.
> cars <- datasets::mtcars
> hc <- hclust(dist(cars),method=”ave”)
> plot(hc)
> hc <- hclust(dist(cars),method=”complete”)
> plot(hc)
> hc <- hclust(dist(cars),method=”single”)
> plot(hc)
Bu şekilde farklı yöntemlerle dendrogramlar çizdirilerek uygun küme sayısı belirlenebilmektedir. Burada üç yöntem denedik. Tam bağlantı yöntemi diğer ikisine göre daha iyi sonuçlar vermekte ve küme sayısının da üç olduğuna karar vererek, dendrogramda üç küme aşağıdaki gibi gözükmektedir.
> rect.hclust(hc,k=3)
Dendrogramları çizdirip karşılaştırmaktan faklı olarak, en iyi kümeleme yöntemini seçmek için tüm yöntemleri aynı anda analiz edebilme imkanını veren “dendexted” paketini yüklemek yeterli.
> install.packages(“dendexted”)
> library(dendextend)
> hclust_methods <- c(“ward.D”, “single”, “complete”, “average”, “mcquitty”, “median”, “centroid”)
> car_list<-dendlist()
> for(i in hclust_methods) {
hc_cars <- hclust(dist(cars), method = i)
car_list <- dendlist(car_list, as.dendrogram(hc_cars))
}
> names(car_list) <- hclust_methods
> car_list
$ward.D
‘dendrogram’
with 2 branches and 32 members total, at height 2594.455
$single
‘dendrogram’
with 2 branches and 32 members total, at height 86.93833
$complete
‘dendrogram’
with 2 branches and 32 members total, at height 425.3447
$average
‘dendrogram’
with 2 branches and 32 members total, at height 245.0744
$mcquitty
‘dendrogram’
with 2 branches and 32 members total, at height 238.1144
$median
‘dendrogram’
with 2 branches and 32 members total, at height 159.2574
$centroid
‘dendrogram’
with 2 branches and 32 members total, at height 162.1535
attr(,”class”)
[1]
“dendlist”
Hangi kümeleme yönteminin birbirine benzer kümeleme sonuçları verdiğini de korelasyon analiziyle görebiliriz.
> install.packages(“corrplot”)
> car_dendlist_cor <- cor.dendlist(car_list)
> car_dendlist_cor
> corrplot::corrplot(car_dendlist_cor, “pie”, “lower”)
oldukça kısa olarak hiyerarşik kümeleme analizi bu şekilde özetlenmiştir.